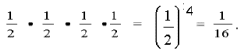Гуманитариям о математике

Цикл рассказов

Бывает, что во время урока математики, когда даже воздух
стынет от скуки, в класс со двора влетает бабочка...

А.П. Чехов

Математика относится к тому роду занятий, стойкое отношение к которым за 6 – 8 лет, проведённых в школе, успевает сложиться у каждого. Нередко отношение однозначное и категоричное. Но не всегда верное.

Одна из причин этого состоит, по-видимому, в том, что многие склонны отождествлять математику с собственным представлением о ней, которое, хотя и складывается зачастую под влиянием случайных обстоятельств, оказывается довольно устойчивым к суровым временным испытаниям.

Но давайте посмотрим, на основании чего это представление формируется у большинства, – конкретные вычисления, задачки по элементарной алгебре, планиметрии и стереометрии. У оканчивающих среднюю школу к этому добавляются некоторые сведения о производной и интеграле. До знакомства же с иными математическими достижениями нашей цивилизации, с математическими открытиями двух последних столетий дело чаще всего не доходит.

Те чувства, которые читатель может испытывать к математике, без всякого сомнения разнообразны. Соответственно различны и используемые им оценивающие слова. Однако стоит честно признать, что не всегда лестная оценка математических дисциплин выпускником средней школы во многих случаях объясняется достаточно просто: он не так хорошо учился и успевал, или в школе его не так интересно учили.

«Если бы только удалось преодолеть то недоверие, с которым весьма многие под влиянием случайных школьных впечатлений сторонятся всего, что связано с математикой, то людей, склонных «импровизировать» в области несложных произведений математического искусства, оказалось бы не меньше, чем активных любителей музыки».

Г. Радемахер, О. Теплиц
«Числа и фигуры»

Но ведь у тех, чьи гуманитарные интересы начали складываться ещё за партой, отношение к математике, выработанное в школе, в последующем особых изменений не претерпевает. А что если рассказать им о некоторых из традиционно опускаемых математических фактов. Тщательно отобрать материал и постараться донести его доходчиво, привлекательно и верно. Учитывая, разумеется, и то, как именно будут воспринимать математические изыски гуманитарно настроенные старшеклассники.

Возможно ли это?

Занятия по математике, проводимые со студентами младших курсов гуманитарных факультетов некоторых российских университетов в течение нескольких последних лет, позволяют нам сказать: да, возможно. Тем более, что грань, разделяющая заканчивающих обучение в средней школе и начинающих обучение в высшей, не так уж и резка.

Преподавание – ремесло не из простых. Снижение возраста обучаемых только умножает трудности. Хотя авторы и накопили определенный опыт общения со студенческой аудиторией, к школьной они обращаются впервые. И потому высказываемые ими суждения не следует рассматривать как бесспорные.

Выбор возможных тем весьма широк. Мы ограничимся рассказами о вероятностях, моделях и играх, о связях геометрии и поэзии.

В 1836 году Пушкин основал ежеквартальный литературный журнал «Совре-менник», на страницах которого ещё при его жизни публиковались Жуковский, Гоголь, Вяземский, Одоевский, Тютчев, Кольцов. Заботясь об облике журнала, Пушкин привлекает к сотрудничеству в «Современнике» и князя П.Б. Козловского, две статьи которого «Разбор Парижского математического ежегодника на 1836 год» и «О надежде», по мнению современников, украсили страницы журнала. Вот как вспоминал начало истории этого сотрудничества сам Козловский:

«Когда незабвенный издатель «Современника» убеждал меня быть его сотрудником в этом журнале, я представлял ему, без всякой лицемерной скромности, без всяких увёрток самолюбия, сколько сухие статьи мои, по моему мнению, долженствовали казаться неуместными в периодических листах, одной лёгкой литературе посвящённых. Не так думал Пушкин ...» [1].

Статья «О надежде» [2] представляет собой первое доступное широкому читателю изложение на русском языке начал (элементов) теории вероятностей и написана столь искусно, что приведённые в ней сведения позволяют вполне успешно решать простейшие вероятностные задачки. Подкупает и глубина понимания излагаемого материала, и горячее стремление автора рассказать о важном при несомненно уважительном отношении к совершенно неподготовленному читателю. И потому в предлагаемом далее рассказе мы неоднократно обращаемся к этой статье Козловского.

Рассказ первый.

Вероятность есть мера надежды

Случайным будем считать всякое событие, которое может либо произойти, либо не произойти в результате некоторого испытания.

Подбрасывается монета – испытание. Выпал герб – событие. Студент сдаёт экзамен (испытание) и получает оценку отлично (событие).

Оценивая возможности исхода того или иного события, мы давно уже привыкли пользоваться словом «вероятность». Словосочетания типа «с вероятностью 50 процентов», или «с вероятностью 1/2», или «в пятидесяти случаях из ста», или «один шанс из двух», или «50 на 50», мы воспринимаем спокойно и с полным пониманием. Даже не подбрасывая монету, мы сразу соглашаемся с тем, что оба исхода – выпадение герба и выпадение решета – равновозможны, более того, мы готовы к оценке результата числом 1/2.

Вообще, та или иная числовая характеристика степени возможности наступления какого-либо определённого случайного события в тех или иных определённых, могущих повторяться многократно обстоятельствах, часто оказывается весьма удобной. Вероятность является одной из таких характеристик.

«Постараемся же найти в числах меру наших надежд ...» [2]

Каждому случайному событию ставится в соответствие число р, 0 Ј p Ј 1 (латинского probabile – вероятное), которое называется вероятностью этого события.

Какие же бывают вероятности?

Статистическая вероятность

Если в одних и тех же условиях при п испытаниях случайное событие А произошло т раз, то отношение

называется относительной частотой события А в п испытаниях.

Обычно при достаточно больших значениях п относительная частота близка к некоторому числу Р(А), которое называют статистической вероятностью события А:

Рассмотрим несколько примеров.

Пример 1. Естествоиспытатель К. Пирсон терпеливо подбрасывал монету и после каждого бросания не ленился записывать полученный результат. Проделав эту операцию 24 000 раз, он обнаружил, что герб выпадал в 12 012 случаях. Вычисляя относительную частоту выпадения герба, получим

что практически равно 1/2.

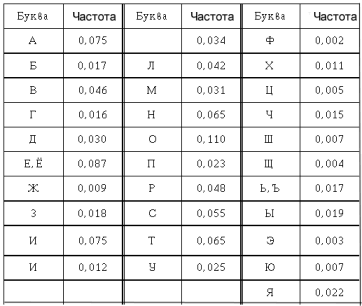
Пример 2. У многих в жизни случается романтическая пора, когда, доверяясь листу бумаги, хочется охранить текст от случайного взгляда. И тогда нередко прибегают к помощи шифра. Однако далеко не всякое зашифрованное сообщение способно выдержать натиск любителя раскрыть его тайный смысл. Например, довольно распространенная практика замены одних букв другими буквами или рисунками не может защитить сокровенный текст от прочтения посторонними. И вот почему – частота появления конкретной буквы алфавита в любом содержательном тексте достаточно большого объема для языка с буквенно-слоговым типом письма является практически постоянной.

В увлекательной форме это описано Артуром Конан Дойлем («Пляшущие человечки») [3] и Эдгаром По («Золотой жук») [4].

В русском языке картина аналогична. Относительная частота появления в тексте букв алфавита описывается следующей таблицей:

Поэтому желающему прочитать зашифрованное письмо достаточно лишь подсчитать частоту появления в нём шифровальных значков разных типов и сопоставить их с частотой букв в этой таблице. Например, если общее число значков в письме равно 1000, а число одинаковых значков некоторого определённого типа окажется равным 55, то, так как = 0,055, за этим значком, скорее всего, скрывается буква «с».

Классическая вероятность

Предположим, что результатом испытания является один из некоторого множества равновозможных исходов (его называют ещё пространством исходов). Если это множество состоит из п элементов, то каждому из равновозможных исходов приписывается число, равное 1/п и называемое его вероятностью.

Такие равновозможные исходы принято называть элементарными событиями.

Пример 3. При бросании монеты пространство исходов можно представить в виде {Г, Р}; каждому из двух исходов приписывается 1/2 (рис. 1). При бросании кубика (игральной кости) пространство исходов имеет вид {1, 2, 3, 4, 5, 6} (рис. 2); каждому из шести исходов приписывается 1/6.

Пример 4. Игра, известная под названием «русская рулетка» (описана М.Ю. Лермонтовым в «Фаталисте» и показана в фильме Оливера Стоуна «Охотник на оленей»), заключается в следующем. Револьвер заряжают одним патроном. Играющий вращает барабан рукой и, приставив к виску, нажимает курок. Если в барабанном магазине 8 патронных гнезд, то выстрел прогремит с вероятностью 1/8.

Пусть п – число всех равновозможных исходов и т – число исходов, составляющих событие А. Тогда вероятностью события А будем считать число

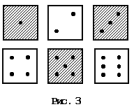– вероятность события А равна отношению числа исходов, благоприятствующих наступлению события А, к числу всех равновозможных исходов.

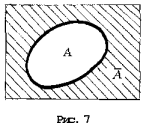
Пример 5. При бросании кости событие А – «выпало нечётное число очков» можно записать как подмножество {1, 3, 5} пространства исходов {1, 2, 3, 4, 5, 6} (рис. 3). Это означает, что если в результате бросания кости выпало нечётное число очков, то событие А произошло. Вероятность этого события нетрудно вычислить: число всех равновозможных исходов п = 6, а число благоприятных событий А – т = 3. Поэтому

Пример 6. В урне находится 7 шаров – 2 белых, 4 черных и 1 красный. Вынимаем один шар наугад. Какова вероятность того, что вынутый шар будет чёрным?

Для простоты рассуждений занумеруем шары. Пусть, например, шары с номерами 1 и 2 – белые, с номерами 3, 4, 5 и 6 – чёрные, а красному шару присвоим номер 7. Так как мы можем вынуть только один из семи шаров, то общее число равновозможных исходов равно семи (п = 7). Из них 4 исхода – появление шаров с номерами 3, 4, 5 и 6 – приведут к тому, что вынутый шар будет чёрным (n = 4). Тем самым, вероятность события А, состоящего в появлении чёрного шара, равна

Можно вычислить вероятность и того, что вынутый шар будет белым (она равна 2/7), и того, что вынутый шар будет красным (1/7).

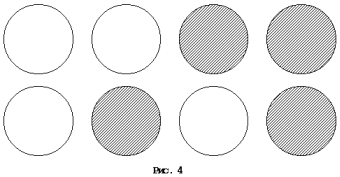
Пример 7. Подбрасывая две монеты – монету N₁ и монету N₂, попробуем ответить на вопрос: какова вероятность одновременного выпадения двух гербов?

Перечислим сначала все возможные исходы нашего испытания:

1) на обеих монетах выпало решето (РР),
2) на монете N₁ выпало решето, а на монете N₂ – герб (РГ),
3) на монете N₁ выпал герб, а на монете N₂ – решето (ГР),
4) на обеих монетах выпал герб (ГГ) (рис. 4).

Из четырёх исходов интересующее нас событие – выпадение двух гербов – наблюдается только в одном. Так как все четыре исхода равновозможны, то вероятность выпадения двух гербов равна 1/4.

Пример 8. Рассмотрим теперь бросание двух костей. Все равновозможные исходы (их число равно 36) можно записать в виде таблицы:

 

 (здесь пара (k, l) означает, что на первой кости выпало k очков, а на второй l).

Вероятность выпадения в сумме 12 очков (событие А) равна .

Выпадение в сумме 10 очков (событие В) возможно в трёх случаях – 4 очка на первой кости и 6 на второй, 5 очков на первой и 5 на второй, 6 очков на первой и 4 на второй. Поэтому вероятность события В (выпадения в сумме 10 очков) равна

Пользуясь приведённой выше таблицей, можно без труда вычислить вероятность выпадения любой суммы очков при однократном бросании пары костей.

Но как быть в случае, когда пара костей бросается на игорный стол несколько раз подряд?

Чтобы научиться отвечать на вопросы, подобные поставленному, опишем некоторые правила, которые позволяют по вероятностям простых событий вычислять вероятности событий более сложных.

Прежде всего, для случайных событий постулируются два основных утверждения:

1. 0 Ј P (A) Ј 1.
2. Р(А) = 1, если А – достоверное событие, и Р(А) = 0, если А – невозможное событие.

Вследствие того, что выпадение 13 очков при бросании пары костей – невозможное событие, его вероятность равна нулю. Выпадение какого-либо числа очков при таком бросании – событие достоверное, его вероятность равна единице.

При общих рассуждениях пространство исходов иногда удобно изображать в виде прямоугольника (рис. 5), каждая точка которого соответствует элементарному событию. Это позволяет рассматривать произвольное событие А как подмножество пространства исходов (рис. 6).

Будем говорить, что в результате испытания произошло событие А, если исход испытания попадает во множество А.

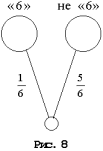
Противоположным называется событие, состоящее в том, что событие А не произошло (рис. 7).

Обозначение:

Пример 9. Если при бросании кости событие А состоит в выпадении «6», то противоположное событие – это невыпадение «6», т.е. выпадение «1», «2», «3», «4» или «5».

Зная вероятность события А, можем найти и вероятность противоположного ему события :

Пример 10. Вероятность выпадения «6» при бросании одной кости равна 1/6, а вероятность противоположного события – невыпадения «6» – 5/6 (рис. 8).

События А и В называются несовместимыми, если они не могут произойти в результате одного и того же испытания.

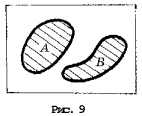
Если события А и В несовместимы, то вероятность суммы этих событий
А + В (произошло либо событие А, либо событие В (рис. 9)) равна

Р (А + В) = Р(А) + Р(В).

Например, если событие А состоит в выпадении «1», а событие В в выпадении «4» на одной и той же кости, то эти события несовместимы: в результате испытания может произойти лишь одно из них. Если же событие А состоит в выпадении «1» на одной кости, а событие В – в выпадении «4» на другой, то эти события совместимы: в результате испытания они могут произойти одновременно.

Пример 11. При бросании двух костей событие А – «выпало десять очков» и событие В – «выпало пять очков» несовместимы. Поэтому вероятность события А + В – «выпало число очков, кратное пяти» можно вычислить двумя способами:

1) по таблице

2) по формуле

Говорят, что событие В зависит от события А, если вероятность события В принимает разные значения в зависимости от того, произошло событие А или не произошло.

Пример 12. Предположим, что при подготовке к экзамену две студентки успели выучить только первые пять билетов из двадцати. Пусть событие А – «первая студентка вытянула один из этих (счастливых для неё) билетов», а событие В – «вторая студентка вытянула счастливый билет».

Если событие А произошло, то среди оставшихся 19 билетов окажется только 4 счастливых, и значит, вероятность события В равна

Если же событие А не произошло, то число счастливых билетов среди оставшихся 19 не изменится, и значит, вероятность события В будет другой:

Тем самым, событие В зависит от события А.

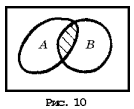
Если события А и В независимы (наступление одного из них никак не влияет на шансы наступления другого), то вероятность произведения этих событий А•В (т.е. того, что события А и В произошли одновременно (рис. 10)) равна произведению их вероятностей:

Р (А•В) = Р(А)•Р(В).

Пример 13 (задача из статьи Козловского).

Мне хочется ехать в Москву, и для того я стараюсь войти приказчиком к одному купцу, который ездил с своим приказчиком всякий год то в Москву, то в Берлин, то в Лондон, то в Париж, то в Италию; теперь задача: каковой меры должна быть моя надежда, выходя из дома, предлагать ему мои услуги?

Событие А (согласие взять князя в приказчики), имеющее вероятность 1/2, и событие В (поездка купца в этом году в Москву), имеющее вероятность 1/5, независимы. Тем самым, вероятность того, что князь таким способом доберется до Москвы, равна

Формула произведения вероятностей применима для трёх и большего числа испытаний. В частности, пользуясь этой формулой, легко вычислить вероятность выпадения герба при каждом из трёх бросаний монеты:

и при каждом из четырёх:

Покажем, как пользоваться приведёнными выше формулами для вычисления вероятностей более сложных событий.