2.6  Метод проекционных операторов Мори

Как следует из приведенных выше результатов, исследование динамики гидродинамических флуктуаций приводит к проблеме вычисления корреляционных функций базисных операторов, т. е. динамических переменных, измеримых с одной стороны, а с другой - достаточных для описания существа рассматривыемых физических явлений. Вычисление этих корреляционных функций является сложной самостоятельной проблемой. По существу, мы продвинулись вперед только в том смысле, что нам удалось свести задачу о релаксации в слабонеравновесной системе к исследованию корреляционных функций, определенных для равновесного состояния.

Принципиальная возможность такого сведения, или, иначе, возможность выразить кинетические коэффициенты слабонеравновесной системы через равновесные корреляционные функции, хорошо известна и является утверждением флуктуационно-диссипационной теоремы (ФДТ).

Физическая причина справедливости ФДТ кроется в том, что микроскопические процессы, вызывающие релаксацию в неравновесной системе и рассасывание флуктуаций в равновесной системе, одни и те же.

Теперь нужно сделать следующий шаг и разработать процедуру вычисления равновесных корреляционных функций операторов, входящих в базисный набор. По существу это несколько иная постановка той же задачи, что уже обсуждалась в разделе 1.4, где мы анализировали причины, по которым оказывается удобным введение операторов проектирования.

Существует много различных определений проекционных операторов, которые используются для построения уравнений движения динамических переменных. Мы начнем знакомство с техникой операторов проектирования с методики, предложенной Мори (см. работу [8]).

Метод операторов проектирования Мори исходит из простой идеи, что любой динамический оператор A(t) можно разделить на две составляющих: одна из них будет выражаться через базисные операторы  P и с-числовые функции, а другая часть будет представлять остаток:

Скалярное произведение двух операторов определено так же, как и раньше [см. формулу (104)]:

Совершенно ясно, что такое разделение является точным и его можно произвести всегда. Весь смысл разделения состоит в том, что операторы PA(t) и QA(t) имеют совершенно разный характер временной зависимости. Операторы P и P⁺ являются квазиинтегралами движения, т.е. почти сохраняющимися величинами, и меняются во времени благодаря лишь относительно слабым возмущениям основного гамильтониана. Что касаетя величины QA(t), то она, наоборот, быстро осциллирует с характерным для атомных масштабов периодом. Именно этот факт позволяет разделить медленную эволюцию оператора и быстрые осцилляции, которые могут определять лишь релаксационные частоты.

Следует сказать несколько слов о том, какой смысл вкладывается в слова медленная эволюция и быстрая эволюция операторов. Дело в том, что уравнение движения для корреляционной функции получается из операторного уравнения, если все его члены умножить справа на некоторый, не зависящий от времени оператор и затем вычислить среднее по равновесному состоянию. Поэтому поведение оператора и поведение корреляционных функций оказываются сопоставимыми.

Смысл оператора проектирования очень легко понять, если воспользоваться геометрической аналогией, представленной на рис. 6 для случая, когда имеется лишь один оператор в наборе P. Используя определение оператора проектирования (119), легко доказать, что выполняется важнейшее условие проектирования вектора на оси ортогонального базиса: операторы PA(t) и (1- PA(t)) ортогональны в смысле скалярного произведения (120):

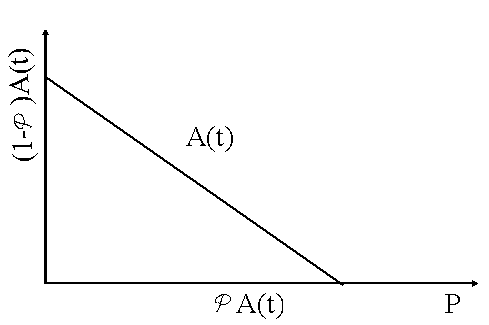
Рис.6. Геометрический смысл оператора проектирования

         Для доказательства соотношения (121) рассмотрим действие оператора проектирования на сопряженный оператор A⁺(t). Используя определение оператора проектирования Мори (119), получаем

Последнее равенство в формуле (122) получается немедленно, если вспомнить, что SP{AB }⁺ = SP{B⁺A⁺ }.Теперь доказательство соотношения (121) сводится просто к учету формулы (122) и выполнению алгебраических преобразований в выражении (121).

Необходимо подчеркнуть, что оператор Q также является идемпотентным проекционным оператором и для него выполняется условие Q² = Q.

Рассмотрим уравнение движения для оператора P, принадлежащего набору базисных операторов:

                   Подействуем на это уравнение оператором Q = (1- P). Поскольку оператор (1- P) не зависит от времени, его можно переставить с оператором дифференцирования по времени. Вводя обозначение Q P(t) = (1- P) P(t) = P^ў(t), получаем

Для упрощения формул удобно ввести обозначение

P P(t) = (P(t), P⁺) (P, P⁺)^-1P = Q(t) P:

С учетом этих определений уравнение (124) можно переписать в виде

       Уравнение (126) может быть легко проинтегрировано. Для этого умножим его слева на операторную экспоненту exp{-(1- P)iLt }. Тогда первые два члена в уравнении (126) могут быть объединены в один, и интегрирование в пределах от 0 до t дает

Этот результат носит промежуточный характер и будет использован несколько позже.

           Рассмотрим теперь уравнение движения для корреляционной функции Q(t) (125). Используя вновь соотношение

получаем:

или

где iW-так называемая матрица частот,

      Рассмотрим скалярное произведение

Поскольку для произвольных операторов C и B выполняется равенство ((1- P)C, B⁺)=0, то скалярное произведение можно записать в виде

         Вспоминая теперь результат (127), запишем уравнение движения для корреляционной функции в виде

Рассмотрим корреляционную функцию

               Учитывая свойства симметрии корреляционных функций при операции эрмитового сопряжения и приведенное выше выражение, получаем

             Наконец, сделаем замену переменных в интеграле, вводя новую переменную s = t₁+t, и определим величину случайной силы f соотношением

С учетом всех сделанных выше замечаний вместо уравнения (131) получаем

             Если учесть, что Q(t) = (P(t),P⁺)(P,P⁺)^-1, то можно легко получить и уравнение движения динамической переменной P(t):

где S(s)-так называемая функция памяти, которая учитывает предысторию развития системы на времена 0 < s < t:

Теперь можно подвести некоторые итоги и обсудить физический смысл полученных результатов. По своему виду уравнения (132), (133) напоминают уравнения Ланжевена для броуновской частицы и описывают немарковскую динамику исследуемых величин P_n.

Важно подчеркнуть, что временная эволюция функции памяти

является негамильтоновой и определяется лишь частью оператора Гамильтона, из которой исключены с помощью оператора проектирования Q члены, определяющие медленную эволюцию динамических переменных.

           Отметим, что произведенное выделение быстро изменяющегося ядра интегральных уравнений части (132), (133) произведено точно. До сих пор не делалось никаких предположений о слабости взаимодействия в системе.

           Наконец, обсудим смысл использования тождественных преобразований, которые мы выполнили при получении уравнений (132), (133). Это представляется необходимым сделать уже сейчас, поскольку у читателей наверняка давно созрел простой вопрос: какой смысл заниматься тождественными преобразованиями динамических уравнений, вводя операторы проектирования, поскольку при этом ничего нового получиться не может?

        На самом деле вопрос достаточно сложный, и для ответа на него вновь придется обратиться к проблеме описания систем , демонстрирующих необратимое поведение, которая уже обсуждалась в главе 1.

             Представляется разумным несколько упростить задачу, рассмотрев ситуацию марковского предела, которая возникает, если считать, что коррелятор случайных сил (134) имеет d- образную временную зависимость. В случае рассмотрения, например, электропроводности такая ситуация возникает, если характерное время взаимодействия частиц при столкновении много меньше времени между столкновениями (напомним читателю, что кинетическое уравнение Больцмана для случая газа малой плотности также является марковским уравнением).

        Подставляя в выражение (133) значение S(s) = G^ў d(s), получаем уравнение движения оператора в марковском пределе

При получении этого выражения мы выделили действительную и мнимую части G^ў:

        Смысл уравнения (2.94a) очевиден. Если G = 0, то динамическая величина P(t) осциллирует с характерной частотой W^ў. Если величина G № 0 , то на прецессию накладывается затухание и величина G имеет смысл обратного времени затухания.

         Таким образом, в этом разделении динамического уравнения на член, описывающий прецессию, и член, описывающий затухание, и состоит основной смысл использования операторов проектирования.

        Наличие члена, описывающего затухание динамической переменной, связано со слабой устойчивостью системы. Действительно, если говорить на языке классической физики, то слабая устойчивость означает, что фазовые точки, находящиеся сколь угодно близко друг от друга, с течением времени разбегаются. Поэтому мы не можем прогнозировать поведение фазовой точки точно, а можем лишь сформулировать некое соотношение неопределенности (мы не знаем точно, где "вынырнет" в следующий момент фазовая точка, а можем указать лишь область, где она появится).

        Та же самая ситуация на квантовом языке выглядит несколько иначе. Если спектр элементарных возбуждений характеризуется действительным значением энергии или частоты, то элементарное возбуждение хорошо определено и существует в неизменном виде сколь угодно долго. Такая система не является диссипативной. Если же элементарное возбуждение хорошо определить не удается и в спектре элементарных возбуждений есть мнимая часть, то возникает некий аналог соотношения неопределенностей, как и в классической системе, только теперь это соотношение неопределенностей связано с тем, что выделить подсистему из окружения не удалось, система находится в смешанном состоянии и является частью некоторой другой системы. По этой причине фазовая поверхность постоянной энергии размывается в некий слой толщиной DE, и мы не можем точно указать значение энергии системы, а это означает, как уже указывалось ранее, потерю информации о системе, а следовательно, её необратимое поведение.

        Вернемся вновь к дальнейшему анализу уравнений движения, полученных методом проекционных операторов Мори.

              Наиболее просто уравнения (132), (133) выглядят, если, выполнив преобразования Лапласа, записать их для лапласовских образов функций Q(t) и P(t). Отсылая читателей за подробностями к специальной литературе (см. [14]), приведем лишь основные соотношения, которые необходимы для выполнения преобразований Лапласа уравнений (132), (133).

Прямое и обратное преобразования Лапласа функции f(x) определяются выражениями

Во второй формуле (136) интегрирование ведется вдоль линии на комплексной плоскости s, для которой Re s = C.

             Для преобразования уравнения (132), (133) нам потребуются еще формулы преобразований Лапласа для производной функции f^ў(x) и для свертки двух функций:

Приведем эти формулы без доказательства [14]:

          Теперь можно записать и результат, который получается, если применить соотношения(136), (137) и произвести преобразование Лапласа уравнений (132), (133). После простых преобразований получаем

              Полученный результат, по существу, не нуждается в комментарии. Действительно, по структуре выражение (138) очень напоминает Фурье-образ автокорреляционной функции, который получается в стандартной схеме записи уравнений движения для функций Грина с последующим использованием метода массового оператора, а величины W    и    S соответствуют действительной и мнимой частям массового оператора.

              Точно так же, как и в случае метода массового оператора, можно произвести разложение корреляционной функции в цепную дробь. Для этого достаточно с функцией S(z) проделать преобразования, приведшие нас от формулы (125) к формуле (138). Таким образом, мы спустимся на этаж ниже. Этот спуск на этаж ниже на самом деле означает учёт более тонких корреляций в системе и естественно может быть продолжен дальше. Фактически получается, что при этом подходе бесконечная цепочка зацепляющихся уравнений записывается в виде разложения в цепную дробь.

       Практическая польза подхода, основанного на применении проекционных операторов Мори для вычисления функций Грина, состоит в том, что для функции памяти S(z) при правильном выборе динамических переменных сразу получается выражение, содержащее взаимодействие по крайней мере во второй степени. По этой причине при вычислении кинетических коэффициентов в борновском приближении теории рассеяния сразу можно опустить взаимодействие с рассеивателями ( фононами, примесями и т.д.) в статистическом операторе и операторах эволюции, и тогда величина S(z) сразу может быть вычислена.

       В следующем разделе мы продемонстрируем использование метода проекционных операторов Мори и метода НСО в простейших случаях для вычисления электропроводности и магнитной восприимчивости системы свободных электронов в проводящих кристаллах.

         Совершенно аналогично можно в принципе найти и полюса функций Грина (117) и (118), определяющие спектр гидродинамических возбуждений в системе, хотя здесь, как уже отмечалось, предварительно необходимо перейти к нормальным координатам, в которых матричная функция Грина становится диагональной.