2.10  Определение неравновесных параметров в методе НСО

       Наше рассмотрение метода НСО является неполным, поскольку мы не обсудили до сих пор главный вопрос о том, как можно определить неравновесные параметры F_n(t), которые задают квазиравновесное и неравновесное распределения.

          Естественно, проблему отыскания неравновесных параметров можно рассматривать в общем виде, не конкретизируя вид системы. Однако, учитывая ограниченный объем учебного пособия, рассмотрим сразу такой физический эффект, который, с одной стороны, является достаточно типичным, а с другой - достаточно простым, чтобы рассмотрение можно было довести до конца.

         Остановим свой выбор на эффекте Оверхаузера, который состоит в том, что при насыщении магнитного резонанса на свободных электронах в металлах или полупроводниках происходит усиление сигнала ядерного магнитного резонанса.

       Эффект Оверхаузера является типичным эффектом и находит достаточно простое объяснение при использовании в качестве параметров F_n(t) эффективных температур зеемановских подсистем электронов проводимостей и ядер.

            С физической точки зрения природа эффекта Оверхаузера весьма проста. Поскольку магнитные подсистемы электронов проводимости и ядер взаимодействуют преимущественно между собой, то их суммарный магнитный момент сохраняется. При насыщении парамагнитного резонанса на электронах проводимости магнитный момент электронной системы будет уменьшаться, и поэтому должен увеличиться магнитный момент ядерной системы. Увеличение магнитного момента ядерной системы проявляется как понижение эффективной температуры ядер, что и приводит к увеличению сигнала ядерного магнитного резонанса.

        Очень похожим является эффект Феера, который состоит в явлении поляризации ядер постоянным электрическим током в полупроводниках. Природа этого эффекта точно такая же. Энергия закачивается здесь в кинетические степени свободы электронов, а затем, в процессах рассеяния с переворотом спина электронов, передается в термостат.

        Можно подметить еще одну особенность эффектов Феера и Оверхаузера. По существу, оба этих эффекта есть пример реализации обычной холодильной машины. Если температура спиновой системы T_s больше температуры кинетических степеней свободы электронов проводимости
T_k, то в каждом элементарном акте рассеяния с участием спинов электронов, ядер и кинетических степеней свободы энергия передается из зеемановской системы электронов в кинетические степени свободы, но при этом отбирается некоторая энергия и у зеемановской системы ядер. В случае эффекта Феера знак поляризации ядер будет другой, поскольку энергия передается из подсистемы кинетических степеней свободы в термостат, и при этом из законов сохранения энергии и импульса следует, что в каждом акте рассеяния несколько больше вероятность изменить ориентацию спина у ядер, находящихся с ориентацией спина вдоль поля, а не наоборот. Это, собственно, и приводит к явлению динамической поляризации ядер.

           Существует еще несколько эффектов, которые можно прекрасно интерпретировать в рамках метода эффективных температур. Это эффекты, в которых при насыщении магнитного резонанса ( на электронах проводимости, донорных примесях или ферромагнитного резонанса в магнитных полупроводниках) наблюдается изменение электрического сопротивления в окрестности резонанса, причем кривая изменения сопротивления точно воспроизводит кривую резонансного поглощения высокочастотной энергии в образце. Конечно, хотя эффект не очень велик и составляет в лучшем случае (для ферромагнитных полупроводников) величину порядка 30%, тем не менее он позволяет детектировать резонанс по изменению электрического сопротивления.

         Следует особо подчеркнуть, что в этом случае речь не идет о повышении температуры всего образца. Увеличивается лишь температура кинетических степеней свободы электронов проводимости.

            После этого краткого качественного обсуждения перейдем к подробному описанию эффекта Оверхаузера.

         Рассмотрим простейший случай, когда неоднородностью электромагнитного СВЧ-поля в объеме образца можно пренебречь. Далее, будем считать, что реализуется достаточно простой случай, когда подсистема длинноволновых фононов, взаимодействующих с электронами, остается в состоянии термодинамического равновесия.

          Для описания неравновесной системы методом НСО необходимо задать гамильтониан системы и выбрать набор неравновесных параметров, характеризующих систему. Представим гамильтониан системы в виде

Гамильтонианы H_e    H_s определены в разделе 2.9.;

w_n-зеемановская частота прецессии ядерных спинов в статическом магнитном поле H, I^a-компонента полного спина ядерной системы, суммирование ведется по всем ядрам со спином I, H_en-гамильтониан контактного электронно-ядерного взаимодействия, который в представлении вторичного квантования по электронным переменным может быть записан в виде

J_q- фурье-образ контактного взаимодействия электронов проводимости с магнитным ядром, x_j-координата ядра со спином I^a_j.

         Наконец, гамильтониан H_ep представляет собой гамильтониан электрон-фононного взаимодействия,явный вид которого приведен, например, в учебном пособии [13].

           Переменное электромагнитное поле с частотой w и амплитудой h(t) будем считать поляризованным в плоскости, перпендикулярной направлению статического поля H. В этом случае гамильтониан взаимодействия зеемановских степеней свободы электронов проводимости с внешним полем будет совпадать с гамильтонианом H_F(t), использованным в предыдущем разделе. Вводя циркулярные компоненты, запишем гамильтониан H_F(t) в виде

Здесь w₁-частота зеемановской прецессии электронного спина в переменном магнитном поле.

               Рассмотрим поведение системы электронов проводимости, фононов и ядерных спинов на временах, больших времени установления равновесия внутри каждой из подсистем. В этом случае справедливо описание подсистем в терминах эффективных неравновесных температур.

           Запишем оператор энтропии (2.11) для рассматриваемой системы в виде

          В формуле (185) b_k(t),   b_s(t),    b_n(t)- обратные температуры кинетических, спиновых степеней свободы электронов проводимости и ядерных спинов, соответственно; b-обратная равновесная температура; z(t)- неравновесный химический потенциал.

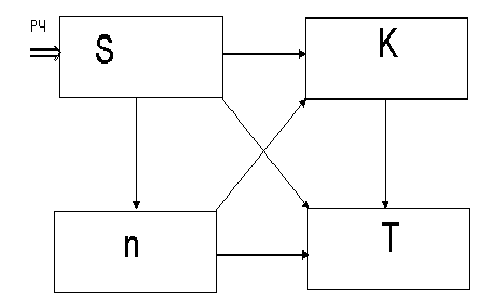
Рис.7. Схема взаимодействия подсистем
кристалла в эффекте Оверхаузера

         Рассматриваемая нами схема взаимодействия подсистем кристалла представлена на рис. 7. Здесь прямоугольниками обозначены выделенные в кристалле подсистемы: S и К - подсистемы спиновых и кинетических степеней свободы электронов проводимости, n - подсистема ядерных спинов, а Т (термостат) - все остальные равновесные степени свободы кристалла.

           Стрелки обозначают каналы передачи энергии между подсистемами, а двойная стрелка изображает накачку радиочастотной (РЧ) энергии в подсистему S. Из приведенной схемы видно, что в принципе может существовать прямой канал передачи энергии из подсистемы n в термостат, но мы этот процесс не будем учитывать. Точно так же и подсистема S может передавать свою энергию в термостат (фононную систему, которая предполагается равновесной) напрямую и в результате электрон-фононного взаимодействия с переворотом спина с участием кинетических степеней свободы кристалла. Хотя прямой канал передачи энергии возможен и соответствующая стрелка изображена на рис. 7, мы его не будем учитывать из-за чрезвычайной неэффективности. В этом смысле стрелка, соединяющая подсистемы S и Т, является лишь напоминанием того, что система электронных спинов может сбрасывать свою энергию в термостат и без участия подсистемы К.

           Для построения системы уравнений баланса энергий подсистем S, K, n, которые в нашем случае будут играть роль обобщенных кинетических уравнений (2.8), необходимо записать выражение для НСО.

         Воспользуемся интегральным уравнением для НСО (148), полученным нами в разделе 2.7. Естественно считать амплитуду радиочастотного поля h малой и ограничиться в уравнениях баланса энергии подсистем членами не выше второго порядка по этому параметру. В этом случае интегральное уравнение для НСО можно записать в виде

          Причина, по которой в правой части первого уравнения формулы (186) неравновесное распределение заменено равновесным, состоит в том, что отклонение неравновесных параметров от их равновесных значений будет второго порядка малости по взаимодействию с внешним электромагнитным полем. Поскольку сам этот член уже содержит первый порядок малости по полю, то отклонением термодинамических параметров от равновесия в этом члене можно пренебречь.

           Второе уравнение в выражении (186) преобразуем, используя результат (101). Как следует из выражения для энтропии (185), термодинамические координаты P_n и термодинамические силы F_n мы выбрали следующим образом:

Следуя формуле (101), найдем уравнения движения для базисных операторов системы с гамильтонианом H. Обозначая, как и раньше,  d/dt A = 1/( i(^h/_2p) ) [A,H], имеем

          Подставим полученные результаты в формулу (101). Учитывая снова тот факт, что отклонения обратных температур db_k, db_s, db_n и химического потенциала dz от равновесных значений пропорциональны второму порядку по взаимодействию, и предполагая, что реализуется стационарный режим, при котором термодинамические параметры dF_n от времени не зависят и поэтому d (d/dtF_n)(t) = 0, перепишем формулу (101) в виде

           Построим теперь с помощью НСО (188) систему макроскопических уравнений баланса энергии подсистем, которые будут использоваться в дальнейшем для отыскания неравновесных температур подсистем кристалла.

           Найдем вначале уравнения движения для операторов энергии подсистем S, K, n относительно полного гамильтониана H(t) = H+H_F(t). Ясно, что для систем К и n уравнения движения будут совпадать с аналогичными уравнениями в выражении (187). Что касается уравнения движения для подсистемы S, то теперь его следует записать в следующей форме:

          Усредняя операторные уравнения движения энергии подсистем S, K, n с учетом того, что в стационарном случае средние значения энергий подсистем не будут зависеть от времени и поэтому в левой части выражения (2.8) частная производная по времени равна нулю, получаем

Корреляционные функции, которые появились в уравнениях баланса, имеют вид

H_e = H_k+H_s. Величина Q_s в уравнении (192) имеет смысл поглощенной спиновой системой электронов РЧ-мощности и выражается через поперечные компоненты высокочастотной магнитной восприимчивости c_+-(w) (176), вычисление которых мы рассмотрели в предыдущем разделе:

          Отметим,что при выводе связанной системы уравнений баланса (191)-(192) мы пренебрегли слабым электронно-ядерным взаимодействием, не существенным с точки зрения кинетики электронной системы.

Решение системы уравнений (191)-(193) позволяет выразить поправки к температурам неравновесных подсистем через корреляционные функции Lij(m) и поглощенную мощность Q_s. Мы не будем обсуждать вопрос о вычислении корреляционных функций Lij(m), поскольку это потребовало бы более глубокого обсуждения механизмов рассеяния электронов в проводящих кристаллах, что выходит за рамки настоящего учебного пособия, и запишем решение системы (191)-(193) в общем виде:

              Из приведенного решения (196) видно, что эффект Оверхаузера проявляется в изменении температуры ядерных спинов при закачке РЧ-энергии в подсистему S. Полный анализ полученного решения с обсуждением всех возможных режимов реализации эффекта Оверхаузера и оценка численных значений для отклонения эффективных температур от равновесных значений представляет прекрасную задачу для самостоятельного решения, и мы оставим эту тему для обсуждения на практических занятиях.

       Полученное решение системы уравнений баланса позволяет найти значение температур неравновесных подсистем S, K, n. Неравновесный химический потенциал может быть найден из условия постоянства числа электронов:

где n-оператор числа частиц. Таким образом, на примере эффекта Оверхаузера мы продемонстрировали возможность построения обобщенных кинетических уравнений и определение параметров, задающих квазиравновесное и неравновесное распределение.

1. Рассмотренные в главе 2 вопросы являются основополагающими для всего дальнейшего изложения, поскольку здесь определены такие ключевые понятия, как неравновесное и квазиравновесное распределения, выведено уравнение движения для НСО, определен проекционный оператор Мори и получены динамические уравнения движения, которым удовлетворяют базисные операторы. Эти результаты широко будут использоваться в последующих главах.
2. Продемонстрированы некоторые примеры возможного применения метода НСО для решения задач физической кинетики. Следует отметить, что примеры эти связаны исключительно с гидродинамическим описанием систем. Причина состоит в том, что метод НСО значительно лучше развит именно для решения таких задач, хотя есть примеры его использования на кинетической стадии эволюции системы [9], [5].
3. С использованием техники проекционных операторов Мори получены обобщенные уравнения движения для динамических операторов и корреляционных функций. Эти уравнения описывают неньютоновую динамику базисных операторов P_n. В следующей главе метод операторов проектирования Мори будет обобщен на случай сильнонеравновесных систем, будет продемонстрировано также совместное использование метода НСО и метода операторов проектирования для построения теории линейного отклика сильнонеравновесной системы.
4. Наконец, в главе 4 будет рассмотрен другой возможный подход построения кинетической теории. В рамках метода основного кинетического уравнения будет построено уравнение движения для квазиравновесного распределения и продемонстрировано использование метода основного кинетического уравнения для вычисления кинетических коэффициентов сильнонеравновесной системы.